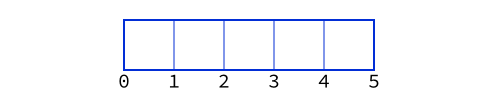
If you’re familiar with nearly any mainstream programming language, and I asked you to draw a diagram of an array, the array indices, and the array elements, odds are good you’d produce a diagram something like this:

In this post, I want to persuade you to replace that image, or, at least, to augment it with an alternate view on the world.

I want to argue that, rather than numbering elements of an array, it makes just as much sense, and in many cases more, to number the spaces between elements:

With this representation, we do have to relearn how to refer to indexing: We refer to A[i] no longer as “The element at index i”, but rather “The element to the right of index i”.

Representing Ranges  🔗︎

I’ll run through a few reasons why I prefer this representation, but most of them boil down to representing ranges of elements.

Suppose we have an array, and we want a way to refer to a certain subset of it, like so:

One obvious answer is with a start and a length: start=2 length=3, but it’s often convenient to represent a range as a pair of (start, end) indices. The latter representation, for example, lets you check if an index falls into the range directly.

If we number elements, it’s not immediately apparent which index to use for end:

Both (1, 3) and (1, 4) seem initially defensible. But if we number between elements, there’s a clear, unique answer:

The indices we want are the ones that lie between the included and excluded elements: (1, 4).

With this model, the rules of range manipulation and comparison become straightforward:

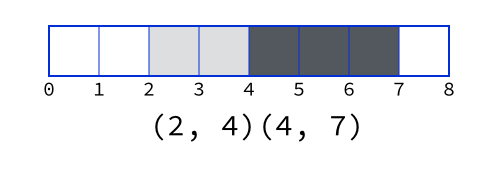
• Two ranges are adjacent if left.end == right.start

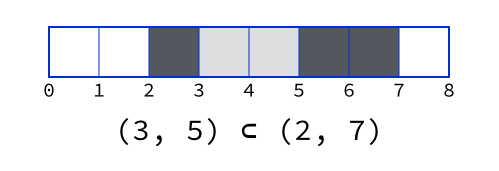
• One range is a subset of another if inner.start >= outer.start && inner.end <= outer.end

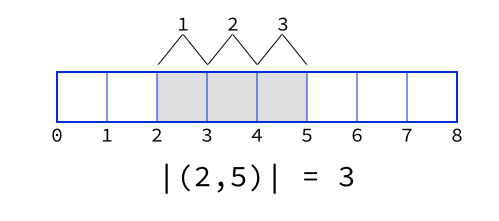
• A range contains end - start elements:

In order to answer the question “if I dereference an index, is the result contained in the range?”, we need to remember that A[i] is now defined as the element after index i. With that in mind, it becomes easy to see that for a range (start, end), elements indexed by start <= i < end are within the range.

Off-by-one errors  🔗︎

Indexing between elements, instead of indexing elements, helps avoid a large class of off-by-one errors. I’ll run through a number of examples using Python, but the fundamental issues apply to array APIs in many more languages, or to any time you’re manipulating an array-like data structure via any of these operations.

Inserting elements  🔗︎

If you want to insert an element into an array, how do you specify the location? If you name an existing element, does the new element go before or after that element?

Python’s standard library documentation somewhat awkwardly specifies that “The first argument is the index of the element before which to insert,” clarifying that this means insert(0, X) inserts X at the start of the array.

But if we number gaps between elements, instead of numbering elements, the story is perfectly clear: 0 names the gap before the first element, and so of course inserting at 0 should prepend an element. Similarly, 1 names the gap between the first and second element, and all the way on.

Slicing arrays  🔗︎

How do we refer to a partial subset of an array that we want to extract? Python, like many other languages, lets you use a pair of indexes:

>>> [1,2,3,4][1:3]
[2, 3]

The documentation, however, has to resolve the same ambiguity noted above: Is the final index excluded or included? Ruby even helpfully offers you both choices:

irb(main)> [1,2,3,4][1...3]
=> [2, 3]
irb(main)> [1,2,3,4][1..3]
=> [2, 3, 4]

As discussed earlier, if we adjust our view of indexes, there is no ambiguity at all. Conveniently, this also gives us the same semantics as Python and most other languages: there are good reasons half-inclusive ranges are generally preferable, and most languages converge on this choice.

Removing elements  🔗︎

If we want to remove a single element from an array, it does seem simpler to index elements directly – we can just name directly the index which we want to eliminate.

However, if we want to adopt the more general primitive, of removing slices, (Python’s del array[x:y]), we run into the same problem as extracting slices, previously. Once again, shifting our thinking to index between elements removes all ambiguity.

Incrementally consuming an array  🔗︎

Suppose we’re walking through an array, consuming it by elements or groups of elements at a time. Perhaps we’re parsing a string, consuming tokens as we go.

How do we keep track of our current position? Should we keep the index of the last element we’ve processed, or of the first element we have yet to process?

If we shift our perspective, this problem too vanishes: We can store the index between the last item consumed, and the next one to be consumed. Our index neatly partitions the buffer into “processed” and “to-be-processed”, with no ambiguity at all.

C/C++ Pointers and Iterators  🔗︎

With pointers in C, or with iterators in C++ (which were essentially designed to mimic C’s pointer semantics), we speak of pointers into an array or of iterators as referring to a specific element in memory.

However, both systems allow for this additional “valid” iterator or pointer, which points “just past the end” of a container. This pointer/iterator does not name a valid element, but is a valid pointer or iterator. The C specification is full of awkward verbiage to address this special-case:

both [pointers] shall point to elements of the same array object, or one past the last element of the array object;

(N1256 §6.5.6p9). And with a C++ std::vector, v.begin() and v.end() are both valid iterators, but v.end() points “one past the end” and cannot be dereferenced.

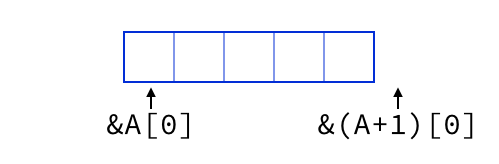
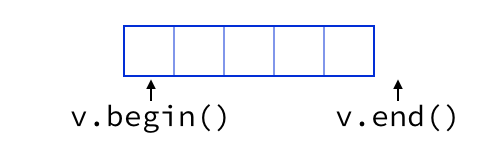
These apparent odd inconsistencies and special cases vanish if you shift your thinking slightly in just the way I’ve been arguing: Instead of thinking of iterators as referring to individual elements, we hold that they name the interstitial points between elements.

If we do so, the “one-past-the-end” iterator is no longer “past” the end – it points directly at the end, which is no more fundamentally special than the “start” iterator which points directly at the beginning.

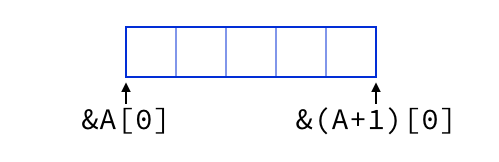
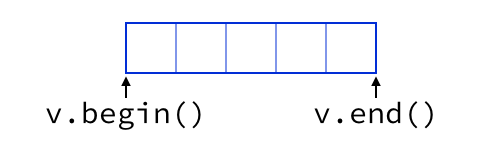
It’s still the case that we cannot dereference v.end(), but that behavior is a function of the “dereference” operation, which selects the element after an iterator. The iterators themselves are no longer special cases.

Postscript: 0 or 1?  🔗︎

It used to be popular, and still is in some circles, to debate whether programming languages ought start array indexing at 0 or 1. And there are still a few holdouts, like Matlab, which number their arrays starting from 1, causing no end of pain and confusion to those poor souls who have to switch between them and more mainstream languages.

Once I started thinking of pointers or iterators or indexes as indexing between elements, one of the more mind-bending realizations that followed was that this model can harmonize the “index from 0” and “index from 1” camps!

Let’s consider an array with interstices labeled again:

The first element, A[0] in C or Python, is bracketed by indexes 0 and 1. The decision, then to name it as 1, does not involve changing the picture at all; If you draw indices between elements, the statement “Arrays start at 1” is simply a decision that “The deference operator refers to the element to the left of an index,” in exactly the same way that I described dereference in a 0-indexed language as taking the element to the right. And presented that way – “should dereference take the left or the right element?” – it becomes clear that 0 or 1 really is an arbitrary choice.

Acknowledgements  🔗︎

I credit my personal shift in thinking – from labeling elements to labeling interstices – to my reading of the excellent The Craft Of Text Editing, which introduces the concept both for its notion of a mark, and specifically as an implementation idea while talking about buffer representations.

I recommend giving the book a read even if you never aspire personally to implement an Emacs; It’s filled with a great number of interesting ideas, and possessed of a profound clarity of thought throughout.